Elliptic Curve Digital Signature Algorithm
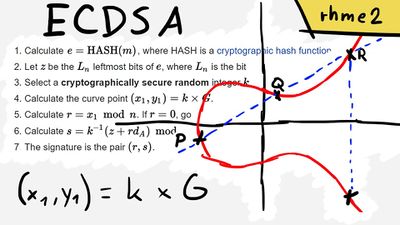
Elliptic Curve Digital Signature Algorithm (ECDSA) is a cryptographic algorithm used by Bitcoin to ensure that funds can only be spent by their rightful owners.
Contents
Descrtiption
Key and signature-size comparison to DSA
As with elliptic-curve cryptography in general, the bit size of the public key believed to be needed for ECDSA is about twice the size of the security level, in bits. For example, at a security level of 80 bits (meaning an attacker requires a maximum of about 280 operations to find the private key) the size of an ECDSA public key would be 160 bits, whereas the size of a DSA public key is at least 1024 bits. On the other hand, the signature size is the same for both DSA and ECDSA: approximately 4t bits, where t is the security level measured in bits, that is, about 320 bits for a security level of 80 bits[1].
Concept
A few concepts related to Elliptic Curve Digital Signature Algorithm:
- private key: A secret number, known only to the person that generated it. A private key is essentially a randomly generated number. In Bitcoin, someone with the private key that corresponds to funds on the public ledger can spend the funds. In Bitcoin, a private key is a single unsigned 256 bit integer (32 bytes).
- public key: A number that corresponds to a private key, but does not need to be kept secret. A public key can be calculated from a private key, but not vice versa. A public key can be used to determine if a signature is genuine (in other words, produced with the proper key) without requiring the private key to be divulged. In Bitcoin, public key are either compressed or uncompressed. Compressed public keys are 33 bytes, consisting of a prefix either 0x02 or 0x03, and a 256-bit integer called x. The older uncompressed keys are 65 bytes, consisting of constant prefix (0x04), followed by two 256-bit integers called x and y (2 * 32 bytes). The prefix of a compressed key allows for the y value to be derived from the x value[2].
- signature: A number that proves that a signing operation took place. A signature is mathematically generated from a hash of something to be signed, plus a private key. The signature itself is two numbers known as r and s. With the public key, a mathematical algorithm can be used on the signature to determine that it was originally produced from the hash and the private key, without needing to know the private key. Signatures are either 73, 72, or 71 bytes long, with probabilities approximately 25%, 50% and 25% respectively, although sizes even smaller than that are possible with exponentially decreasing probability.
Security
In December 2010, a group calling itself fail0verflow announced recovery of the ECDSA private key used by Sony to sign software for the PlayStation 3 game console. However, this attack only worked because Sony did not properly implement the algorithm, because k was static instead of random. As pointed out in the Signature generation algorithm section above, this makes dA solvable and the entire algorithm useless.
On March 29, 2011, two researchers published an IACR paper demonstrating that it is possible to retrieve a TLS private key of a server using OpenSSL that authenticates with Elliptic Curves DSA over a binary field via a timing attack. The vulnerability was fixed in OpenSSL 1.0.0e.[3]
In August 2013, it was revealed that bugs in some implementations of the Java class SecureRandom sometimes generated collisions in the k value. This allowed hackers to recover private keys giving them same control over bitcoin transactions as legitimate keys’ owners had, using the same exploit that was used to reveal the PS3 signing key on some Android app implementations, which use Java and rely on ECDSA to authenticate transactions.
This issue can be prevented by deterministic generation of k, as described by RFC 6979.
Sources
- https://en.bitcoin.it/wiki/Elliptic_Curve_Digital_Signature_Algorithm
- Elliptic Curve Digital Signature Algorithm – Wikipedia article
See Also on BitcoinWiki
- Block hashing algorithm
- Bitstate hashing
- Symmetric-key algorithm
- Luhn mod N algorithm
- Forney algorithm
- RC algorithm